티스토리 뷰
정렬(Sort)은 알고리즘 과목에서 항상 단골로 출제되는 영역입니다. 오늘은 그 중에서 힙 정렬(Heapsort)를 알아보도록 하겠습니다. 우선 이 정렬 알고리즘을 이해하기 위해서는 힙(heap)이라는 독특한 자료구조에 대해 먼저 이해 해야 합니다.
그런데 이 heap을 알려면 우선순위큐(Priority Queue)를 또 먼저 알아야 합니다. 그러면 또 그냥 큐(Queue)가 뭔지도 알아야겠죠. 점점 일이 복잡해 지니까 아주 단순하게 설명하도록 하겠습니다. 각각의 개념에 대해 부족한 설명은 추후에 (가능하다면)포스트 하도록 하겠습니다.
큐(Queue)는 컴퓨터의 기본적인 자료구조의 일종입니다. 먼저 삽입된 데이터가 먼저 나오는 FIFO(First In First Out)구조로 되어 있는데 화장실 앞에 줄을 선 사람들을 연상하면 쉽게 이해할 수 있습니다. 먼저 줄을 선 사람이 먼저 볼 일을 보고 나오는 것 처럼 먼저 들어간 데이터(혹은 작업)이 먼저 나오는 것이죠.

그런데 아주 위급한(곧 분출이 시작되는) 상황에 처해 계신 분이 줄의 맨 끝에 섰습니다. 이 분이 화장실 안이 아니라 밖에서 분출을 시작하는 장면을 라이브로 보고 싶은 사람은 드물기 때문이 사람들은 이 위급하신 분께 차례를 양보해 드렸습니다.
이렇게 줄을 서 있는 사람에게 차례를 양보하는 것, 다시말해 우선순위를 주는 것 처럼 큐 안에 데이터 들에도 우선순위를 주고 그 우선순위가 높은 데이터가 먼저 처리되도록 하는 자료구조를 우선순위 큐(Priority Queue)라고 합니다.
그렇다면 우선순위 큐는 어떻게 구현할 수 있을까요? 가장 쉽게 생각할 수 있는 방법은 아마 LinkedList나 배열 같은 것을 이용해서 데이터 마다 우선순위를 같이 저장하고 원소를 꺼낼 때 마다 모든 원소를 순회해 우선순위가 가장 높은 원소를 찾는 방법이겠지요. 이렇게 하면 원소를 추가하는데는 O(1), 원소를 꺼내는 데는 O(n)의 시간이 걸리게 됩니다.
그러나 언제나 원소를 꺼낼 때 마다 O(n)의 시간이 걸린다면 데이터가 많아지고 꺼내는 횟수가 늘어날 수록 시간이 너무 지연됩니다. 조금 더 빠르게 데이터를 꺼낼 수 있는 방법이 필요했고 그래서 등장한 것이 바로 힙(heap)입니다. 힙은 결국 우선순위 큐를 구현하기 위한 자료구조 입니다.
힙, Heap
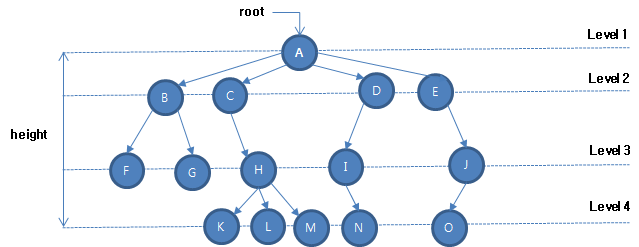
힙(Heap)은 힙 트리(heap tree)라고도 불리는데, 그것은 힙이 트리(Tree), 그 중에서도 완전 이진 트리(Complete binary tree)의 형태를 띄고 있기 때문입니다. 그렇다면 또 완전 이진 트리가 무엇인지 잠깐 살펴 봐야겠죠?
위 그림처럼 트리(Tree) 구조를 가진 것들 중에 각각의 노드가 최대 두 개의 자식 노드만을 가지는 것을 이진트리(binary tree)라고 합니다. 그런데 이 트리의 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있고, 마지막 레벨의 노드는 가능한 왼쪽에 있는 것을 완전 이진 트리(complete binary tree)라고 합니다.
완전이진트리 구조를 이용하면 원소를 입력하고 찾는 데 걸리는 시간을 O(logN)만에 수행 가능합니다. 이런 완전이진트리의 특성을 이용하면 우선순위 큐를 아주 쉽게(혹은 빠르게) 구현할 수 있는데 그것이 바로 힙입니다. 그런데 우선순위 큐는 '우선순위'에 따라 출력이 다르게 나온다는 말씀을 이미 드렸습니다. 그렇다면 힙은 우선순위를 어떤식으로 결정하게 될까요?
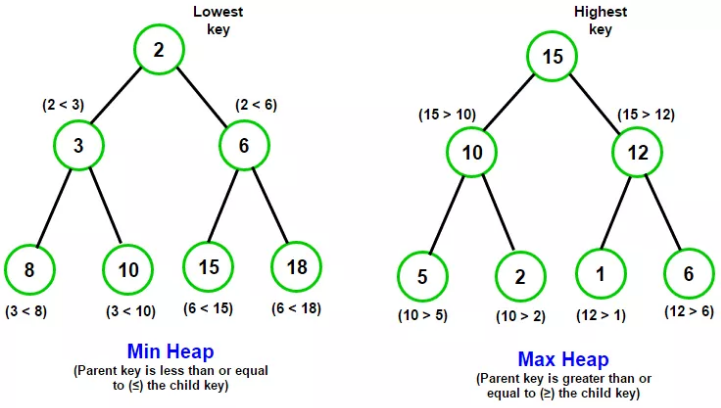
힙에는 두 가지 종류가 있습니다. 최대 힙(max heap)과 최소 힙(min heap)입니다. 최대힙은 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진트리를 나타냅니다. 반대로 최소 힙은 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진트리를 나타냅니다.
이 최대힙 혹은 최소힙을 이용하면 항상 첫번째 노드의 키 값을 최대, 혹은 최소값으로 유지할 수 있게 됩니다. 최대값을 찾는 시간 O(1)로 줄일 수 있는 것이죠. 완전 이진 트리 구조를 하고있기 때문에 삽입에는 O(logN)이 걸립니다. 이전의 배열이나 리스트를 이용하는 방법에 비해 훨씬 빨라진 것을 알 수 있습니다.
힙의 구현

위 그림은 최대 힙이 실제로 어떤식으로 구현되는지를 보여주고 있습니다. 그림 (a)에서 마지막 레벨에 있는 4가 그림 (b) 처럼 15로 바뀌었다고 해 보겠습니다. 그러면 먼저 15와 상위 노드인 8을 비교합니다. 최대 힙은 항상 상위 노드가 하위 노드보다 더 큰 값을 가지고 있기 때문에 더 큰 값을 가진 15가 상위 노드와 위치를 바꾸게 됩니다. 그 결과가 그림 (c) 입니다. 그리고 다시한 번 상위노드은 14와 비교를 하고 그림(d)와 같이 상위노드와 교환되게 됩니다. 마지막으로 루트인 16과 비교했을 때는 15가 더 작은 숫자이므로 바꿀 이유가 없기 때문에 그림 (d)에서 멈추게 됩니다.
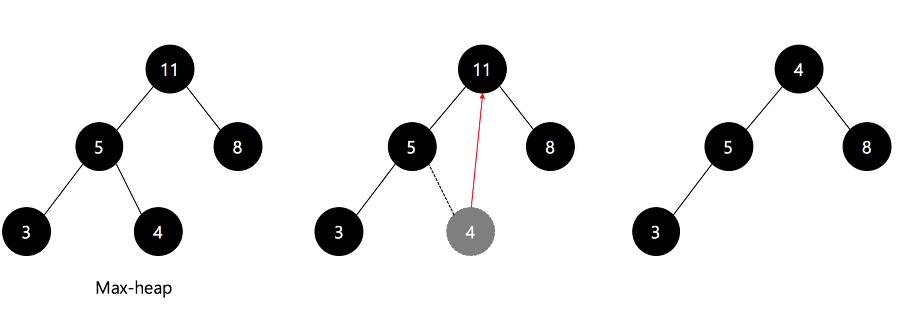
반대로 데이터가 삭제되는 경우는 어떨까요? 이 때는 삭제된 노드에 마지막 레벨의 마지막 값을 옮깁니다. 그리고 자식 노드들 중 더 큰 노드와 자리를 바꿉니다. 더이상 자신보다 더 큰 자식 노드 값이 없으면 종료됩니다. 이 삽입 삭제 연산이 모두 O(logN)만에 일어난다는 것을 알 수 있습니다. 힙은 이런식으로 우선순위를 유지하게 됩니다.
힙 정렬(Heapsort)
힙에 대해서 알았으니 이제 힙 정렬(Heapsort)에 대해서도 조금 감이 잡힐 것입니다. 힙이라는 자료구조는 항상 최 상위 노드값이 최대거나 최소입니다. 최 상위 노드 값을 하나씩 뽑아내면서 정렬을 하는 것이 바로 힙 정렬입니다. 따라서 힙 정렬의 수행 방법은 다음과 같이 구성됩니다.
- 원소들을 입력하여 최대 힙 구성
- 힙에 삭제 연산을 수행하여 얻은 원소를 마지막 자리에 배치
- 나머지 원소에 대해서 최대힙 구성
이 과정을 그림으로 보면 아래와 같습니다.
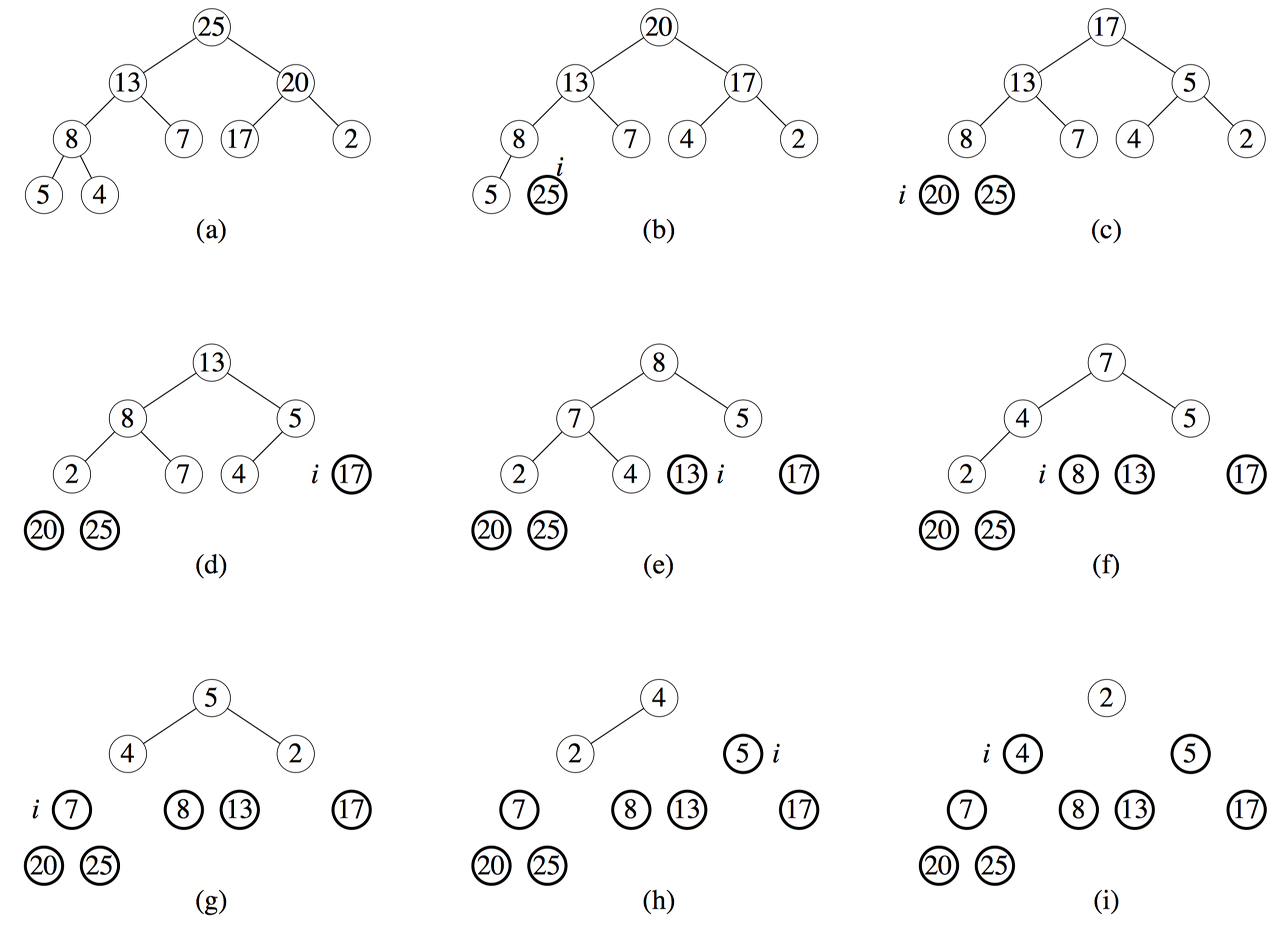
(a)에서 1번 단계인 최대힙을 구성합니다. 그리고 최대값인 루트노드를 제거하여 가장 마지막 자리에 넣고 남은 트리에 대해 다시 최대힙을 구성합니다. 그것이 (b) 입니다. 이 과정을 반복하면 결국 마지막에는 (i)와 같이 정렬된 배열을 얻을 수 있게 됩니다.
결국 힙 정렬에서 중요한 것은 정렬 알고리즘 그 자체가 아니라 힙이라는 자료구조의 이해라고 할 수 있을 것 같습니다.
'algorithm' 카테고리의 다른 글
| 이분탐색(binary search) (5) | 2019.06.29 |
|---|---|
| 카드게임 문제 (1) | 2019.05.15 |
| N으로 표현 (1) | 2019.02.28 |
- Total
- Today
- Yesterday
- 문장 생성기
- 크롬
- 야근
- 마르코프 연쇄
- 코딩의 기술
- restful api
- 자바스크립트 개론
- markov chain
- 클린코드
- Spring in Action
- Count
- java
- 경고
- 자바스크립트개론
- 유지보수
- 동적계획법
- was
- RESTful
- 몰라서망신
- Markov
- Warning
- 전략패턴
- REST API
- 로그
- GROUP BY
- html
- CONVENTIONS
- 마르코프
- DP
- 디자인패턴
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
